--> Le nombre d'Or En architecture Dans l'architecture grecque classique, le nombre d'or est souvent cité.
Voici un article publié par Par Morgane Cariou & Adèle Jatteau sur le site Archéologie en chantier, que l'on peut retrouver en cliquant ici.
Les remarques qui apparaissent ne font pas partie du corps de l'article original.
Le nombre d’or dans l’architecture grecque : mythe ou réalité ?
L’idée que le nombre d’or est un élément déterminant de l’architecture grecque antique est largement répandue, et relayée par des arguments plus ou moins scientifiques. C’est cette idée que tente d’interroger cet article en inspectant les sources antiques et les commentaires contemporains.

Filles des nombres d’or,
Fortes des lois du ciel,
Sur nous tombe et s’endort,
Un Dieu couleur de miel.

Paul Valéry, « Cantique des Colonnes ».

Le nombre d’or est un nombre égal à $\dfrac{1+\sqrt{5}}{2}$, soit environ $1,618$ et correspond à une proportion considérée comme particulièrement esthétique. Il apparaît dans la pensée grecque avec Pythagore, au tournant du VIème et du Vème siècle avant J.-C. mais Euclide, dans ses Eléments, est le premier à développer une théorie de ce nombre dans le passage où il tente de définir la façon la plus logique de couper harmonieusement un segment en deux parties inégales.

Cette proportion, pour de nombreux artistes comme Léonard de Vinci ou encore Le Corbusier -pour ne citer que les plus célèbres-, donnerait la clef de l’harmonie d’une œuvre d’art.
Cette croyance est d’autant plus largement répandue depuis la parution dans les années 1930 du livre du Roumain Matila Ghyka intitulé Le Nombre d’Or. Pour cet auteur, les artistes grecs de l’Antiquité utilisaient délibérément le nombre d’or, ou section dorée, pour déclencher l’émotion du spectateur. Cela expliquerait que la statuaire et l’architecture de la Grèce classique -le Parthénon, les Propylées- s’adressent si merveilleusement à nos sens. Et Valéry fut un des fervents admirateurs de Ghyka, convaincu aisément de la véracité de ses thèses.

Mais dans quelle mesure n’y a-t-il pas là un mythe architectural ? Trouve-t-on réellement la proportion divine dans l’architecture grecque ?

Quelques propriétés mathématiques A=[-9,0] B=[9,0] C = [2,0] point(A) point(B) point(C) segment(A,B) texte("a",[-3.5,1]) texte("b",[5.5,1]) trait = 0.2 for(i=-3;i<2;i=i+0.1){ point([i-2,1/(0.2+Math.pow(Math.E,i-4))-6.5]) } for(i=-3.5;i<1.5;i=i+0.1){ point([i+3.5,1/(0.2+Math.pow(Math.E,-i-5.5))-6.5]) } for(i=-2.0;i<2;i=i+0.1){ point([i+7,-1/(0.2+Math.pow(Math.E,i-4))+3.45]) } for(i=-2.0;i<2;i=i+0.1){ point([i-7,-1/(0.2+Math.pow(Math.E,-i-4))+3.45]) } texte("a+b",[-0.75,-6.5]) La section d'or La définition géométrique de la section dorée par Euclide est celle qui coupe un segment $a + b$ en établissant une relation telle que : $ \dfrac{a + b}{a} = \dfrac{a}{b}$.
Il l’appelle « proportion de moyenne et d’extrême raison ». Si on pose $x=\dfrac{a}{b}$, on a alors que $\dfrac{1}{x}=\dfrac{b}{a}$ et :
$ \dfrac{a + b}{a}$ $=$ $\dfrac{a}{b}$
$ \dfrac{a}{a}+\dfrac{b}{a}$ $=$ $\dfrac{a}{b}$
$ 1+\dfrac{1}{x}$ $=$ $x$
$x\left( 1+\dfrac{1}{x}\right)$ $=$ $x\times x$
$x^2-x-1$ $=$ $0$.
Désigné par la lettre grecque $\varphi$ en l‘honneur du sculpteur grec Phidias, qui l‘aurait utilisé pour concevoir sa statue d’Athéna décorant le Parthénon, le nombre d’or est un nombre algébrique incommensurable, irrationnel, aux caractéristiques uniques :

• c’est la racine positive de l’équation $x^2 - x - 1 = 0$.

• pour calculer le carré du nombre d’or, il suffit de lui rajouter 1 : $\varphi+1=\varphi^2$.

• pour calculer l’inverse du nombre d’or, il suffit de lui retrancher 1 : $\varphi-1=\dfrac{1}{\varphi}$.

La célèbre suite de Fibonacci, mathématicien du XIIIème siècle, entretient des liens étroits avec $\varphi$. Elle est construite sur la raison suivante : chaque nombre de la suite s’obtient en additionnant les deux nombres précédents de la suite. Ainsi la suite partant de $0$ est : $1$, $1$, $2$, $3$, $5$, $8$, $13$, $21$, $34$...
Or le rapport entre deux termes qui se suivent tend de plus en plus précisément vers $\varphi$ :

$\dfrac{5}{3} = 1,666$, $\dfrac{13}{8} = 1,625$, $\dfrac{144}{89} = 1,6179$ ...
D’autre part, on retrouve la suite de Fibonacci dans les puissances de $\varphi$ :

• $\varphi^3 = \varphi\times\varphi^2$ $=$ $\varphi(\varphi+1)$ $=$ $\varphi^2+\varphi$ $=$ $2\varphi+1$.

• $\varphi^4 = \varphi^3\times\varphi$ $=$ $(2\varphi+1)\varphi$ $=$ $2\varphi^2+\varphi$ $=$ $2(\varphi+1)+\varphi$ $=$ $3\varphi+2$.

• $\varphi^5 = 5\varphi+3$.

• $\varphi^6=8\varphi+5$.

• $\varphi^7=13\varphi+8$

Chaque terme de la série est égal à la somme des deux termes précédents et les coefficients sont les nombres de la suite de Fibonacci.

En géométrie, le nombre d’or sert à la construction de diverses figures, et notamment du pentagone étoilé et du pentagone convexe (pentagramme), figure de référence et signe de ralliement des pythagoriciens.
Le pentagone régulier est une figure d’or car la proportion entre une diagonale et un côté est le nombre d’or : $\frac{AC}{AB} = \varphi$. a = 2*%PI/5 r = 8 for(i=1;i<6;i++){ x = r*cos(i*a) y = r*sin(i*a) point([x,y]) segment([x,y],[r*cos((i+1)*a),r*sin((i+1)*a)]) segment([x,y],[r*cos((i+2)*a),r*sin((i+2)*a)]) } texte("A",[2.3,8]) texte("C",[2.3,-8.5]) texte("B",[8.3,0]) Si on considère le cercle trigonométrique de centre $O$, et les points $A$ et $B$ et $C$ de la figure précédente, d'affixe respective, $z_a$, $z_B$ et $z_C$ on a :
$z_A=\text{e}^{\frac{2\text{i}\pi}{5}}$, $z_B=1$ et $z_C=\text{e}^{-\frac{2\text{i}\pi}{5}}$.

On peut également considérer les coordonnées de ces points sans utiliser les nombres complexes avec :

$A\left(\cos\left(\dfrac{2\pi}{5}\right)\,;\sin\left(\dfrac{2\pi}{5}\right)\right)$ ; $B(1\,;0)$ ; $C\left(\cos\left(-\dfrac{2\pi}{5}\right)\,;\sin\left(-\dfrac{2\pi}{5}\right)\right)$.

On détermine les longueurs des segments soit avec la formule utilisant les modules des nombres complexes, soit avec la formule de la classe de 2nde.
On utilise également les valeurs des cosinus et sinus de l'angle $\dfrac{2\pi}{5}$, la formule $\cos^2(\theta)+\sin^2(\theta)=1$ et la parité des fonctions trigonométriques.

$AC$ $=$ $\sqrt{\left( \cos\left(-\dfrac{2\pi}{5}\right)-\cos\left(\dfrac{2\pi}{5}\right)\right)^2+\left( \sin\left(-\dfrac{2\pi}{5}\right)-\sin\left(\dfrac{2\pi}{5}\right) \right)^2}$
$=$ $\sqrt{\left( \cos\left(\dfrac{2\pi}{5}\right)-\cos\left(\dfrac{2\pi}{5}\right)\right)^2+\left( -\sin\left(\dfrac{2\pi}{5}\right)-\sin\left(\dfrac{2\pi}{5}\right) \right)^2}$
$=$ $\sqrt{\left( -2\sin\left(\dfrac{2\pi}{5}\right) \right)^2}$
$=$ $2\sin\left( \dfrac{2\pi}{5} \right)$
$=$ $\dfrac{\sqrt{2}}{2}\sqrt{5+\sqrt{5}}$.
$AB$ $=$ $\sqrt{\left(1-\cos\left(\dfrac{2\pi}{5}\right)\right)^2+\sin^2\left(\dfrac{2\pi}{5}\right)}$
$=$ $\sqrt{2-2\cos\left(\dfrac{2\pi}{5} \right)}$
$=$ $\sqrt{2-\dfrac{\sqrt{5}-1}{2}}$
$=$ $\sqrt{\dfrac{5-\sqrt{5}}{2}}$
$=$ $\dfrac{\sqrt{2}}{2}\sqrt{5-\sqrt{5}}$.


Ainsi :
$\dfrac{AC}{AB}$ $=$ $\dfrac{\sqrt{5+\sqrt{5}}}{\sqrt{5-\sqrt{5}}}$
$=$ $\dfrac{\sqrt{5+\sqrt{5}}}{\sqrt{5-\sqrt{5}}}\times\dfrac{\sqrt{5-\sqrt{5}}}{\sqrt{5-\sqrt{5}}}$
$=$ $\dfrac{\sqrt{ (5+\sqrt{5})(5-\sqrt{5}) }}{5-\sqrt{5}}$
$=$ $\dfrac{\sqrt{ 25-5 }}{5-\sqrt{5}}$
$=$ $\dfrac{\sqrt{ 20}}{5-\sqrt{5}}$
$=$ $\dfrac{\sqrt{ 20}}{5-\sqrt{5}}\times\dfrac{5+\sqrt{5}}{5+\sqrt{5}}$
$=$ $\dfrac{2\sqrt{ 5}(5+\sqrt{5})}{25-5}$
$=$ $\dfrac{\sqrt{ 5}(5+\sqrt{5})}{10}$
$=$ $\dfrac{5\sqrt{ 5}+5}{10}$
$=$ $\dfrac{\sqrt{ 5}+1}{2}$
$=$ $\varphi$.

$\varphi$ dans l’architecture grecque

Le cas le plus flagrant est peut-être celui du théâtre d’Epidaure, construit en Grèce à la fin du IVème siècle avant J.-C. Il y a en effet 55 gradins répartis en deux séries de 34 et 21 rangs ; or ce sont trois nombres successifs de la suite de Fibonacci et les rapports 34/21 et (34+21)/34 sont très proches du nombre d’or. Les gradins semblent donc partagés en « extrême et moyenne raison » Théâtre d’Epidaure A Delphes, la présence de la suite de Fibonacci, déjà remarquée dans des temples du Vème siècle, a été mise en évidence dans la Tholos de Marmaria, dont les colonnes ont été implantées grâce à des polygones inscrits dans un cercle, une figure parfaite selon la théorie des Pythagoriciens, car sa composition est régulière. La façade du Trésor de Cyrène, selon une nouvelle restitution, est inscrite dans un carré découpé en rectangles dont les rapports seraient proche du nombre $\varphi$.

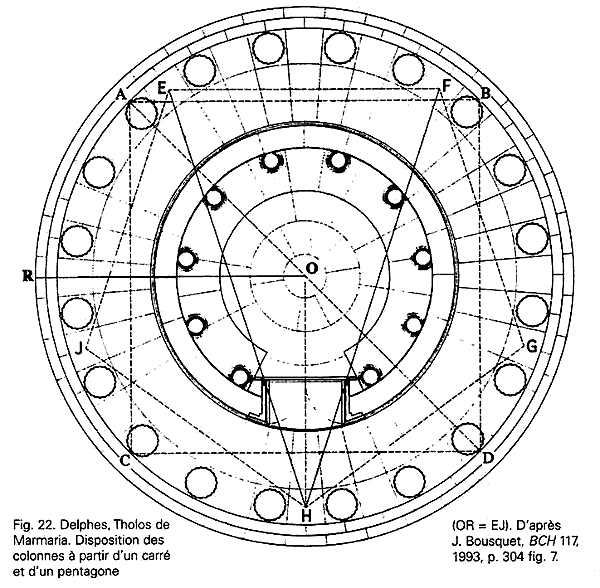
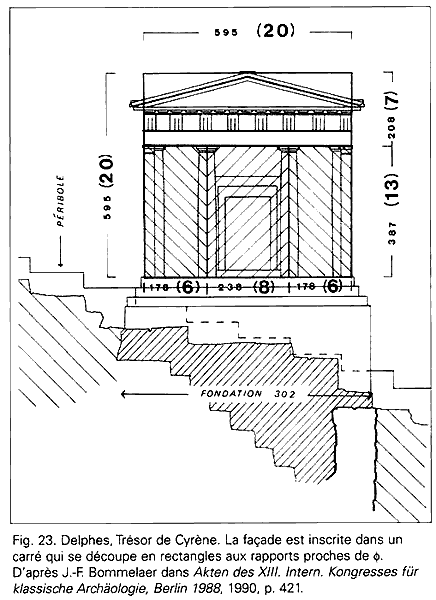
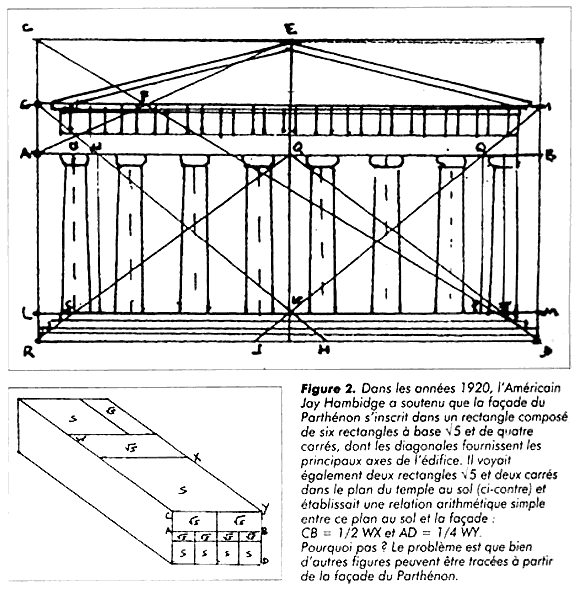
La référence au nombre d’or a également été supposée dans la construction du temple dit de Héra II à Poseidonia (Lucanie), dont la façade s’inscrit dans un ensemble de pentacles assez complexe. La Tholos de Delphes. Le Trésor de Cyrène Le plus célèbre des monuments étudiés sous le rapport du nombre d’or est le Parthénon. Pour ce monument, J. Hambidge, F. Lund et E. Moessel, principaux auteurs à avoir cherché la Divine Proportion dans l’architecture grecque, restituent 3 types de tracés géométriques différents, mais qui font tous appel au rapport (1+√5)/2. Ainsi F. Lund voit dans la façade un pentagone régulier et un pentagramme inscrits dans un cercle, lui-même inscrit dans un carré. Le problème est que l’on pourrait tracer bien d’autres figures à partir des plans de tous ces monuments et que le nombre d’or semble être présent au même titre que d’autres chiffres très fréquents. Le Parthénon Le nombre d’or, un mythe ?

Le diplomate roumain Matila Ghyka, dans Le Nombre d’or, s’autorise de ces travaux pour fonder l’architecture grecque sur le rectangle à module $\varphi$. Nombre d’auteurs, dans son sillage, ont été séduits par cette thèse qui s’appuie sur les pythagoriciens, et ont eu recours à la section d‘or pour réaliser leurs oeuvres.

Pourtant, selon Marguerite Neveux, ce mythe ne résiste pas à un examen attentif : par exemple, Ghyka se fonderait sur des mesures approximatives. La preuve en est que pour trouver le rectangle d’or dans la façade du Parthénon, il est obligé de prendre quelques marches en plus de la façade elle-même.

De plus, Ghyka est conduit à une généralisation abusive de sa théorie à toute l’architecture grecque et même à l’architecture égyptienne, alors que l’idée même de nombre d’or apparaît, avec la notion de proportion, seulement à partir de la géométrie grecque (VI-Vèmes siècles avant J.-C. en Italie du Sud).

N’est-il donc pas plus prudent de substituer la notion de proportion à celle, plus systématique, plus biaisée, de nombre d’or ?

En effet, le recherche de proportions harmonieuses, que ce soit en architecture, dans la sculpture ou même dans le monde, est inhérente à la civilisation grecque. Pythagore, à l’aube du siècle de Périclès, a fondé une école de pensée basée sur les nombres et leurs rapports qui a largement influencé la mentalité grecque. En attribuant un nombre à chaque chose, les pythagoriciens font du nombre le concept central de la nature. Ainsi lit-on dans Jamblique : « les acousmaticiens (élèves des pythagoriciens), dont était responsable Hippase, ont dit du nombre qu’il est le modèle premier de la création de l’univers. » On le voit donc, le nombre est au centre de la pensée grecque, et ce dès l’époque de Pythagore.

C’est pourquoi on peut relever sans crainte d’interprétation abusive la récurrence de proportions supposées harmonieuses dans les monuments du siècle de Périclès et notamment, si l’on en croit le théoricien latin Vitruve, dans son livre intitulé De architectura, le module √5. Les architectes grecs travaillaient à partir d’unité modulaire ou modulus, c’est-à-dire du rapport, unique de préférence, qui permet d‘établir des relations numériques entre toutes les mesures d‘un édifice et l‘ensemble. Selon Vitruve qui en parle longuement, l’origine du système modulaire se trouverait dans les proportions du corps humain, dont les membres seraient commensurables entre eux : 1 pied = 1/6 de la taille d’un homme, qui serait elle-même égale à la largeur de ses bras tendus à l’horizontale (= 1 brasse). La colonne dorique devait faire, lors de sa création, une hauteur égale à 6x son diamètre, alors que la colonne ionique, sentie comme une silhouette féminine plus élancée, devait faire 8x son diamètre en hauteur. C’est grâce à ce système rationnel de proportions ou analogia, qui régit tout le bâtiment, qu’on peut atteindre l’harmonie perceptible à l’œil comme la musique à l’oreille.

En somme, le nombre d’or est une réalité mathématique, découverte par les Pythagoriciens et connue, selon toute vraisemblance, des architectes grecs. L’ensemble des monuments qui ont survécu au temps témoigne indéniablement d’une attention aux proportions qui va jusqu’à l’utilisation de légères distorsions architecturales visant à créer des effets d’optique allant dans le sens d’une plus grande harmonie encore. Mais l’idée que le nombre d’or est, pour ainsi dire, la pierre angulaire de l’architecture grecque relève d’une systématisation exagérée, historiquement datée. Quant aux calculs vitruviens, ils restent théoriques, et il est rare, dans la pratique, d’arriver à reconstituer de manière convaincante le système modulaire d’un monument. Il est préférable d’établir ici que l’architecture grecque témoigne d’une recherche de rapports harmonieux et réguliers.
La suite de Fibonacci La suite de Fibonacci a été introduite par Léornado de Pise, dit Fibonacci, en 1202 dans son ouvrage le Liber Abaci.
Voici une traduction de Jérôme Gavin et Alain Schärlig du problème la présentant.
« Quelqu’un a déposé un couple de lapins dans un certain lieu, clos de toutes parts, pour savoir combien de couples seraient issus de cette paire en une année, car il est dans leur nature de générer un autre couple en un seul mois, et qu’ils enfantent dans le second mois après leur naissance. »
La résolution de cette exercice, en notation moderne, fait intervenir la suite $(u_n)$ ci-dessous :
$u_0=u_1=1$ et pour tout entier $n$, $u_{n+2}=u_{n+1}+u_n$.

Les premiers termes de la suite sont donnés dans le tableau ci-après :
$n$ $0$ $1$ $2$ $3$ $4$ $5$ $6$ $7$ $8$
$u_n$ $1$ $1$ $2$ $3$ $5$ $8$ $13$ $21$ $34$
Notre objectif est de déterminer l'expression de $u_n$ en fonction de $n$, puis la limite du rapport $\dfrac{u_{n+1}}{u_n}$.

Observons tout d'abord un algorithme qui calcule et affiche n'importe quel terme de la suite de Fibonacci et qui permet de calculer les rapports entre deux termes consécutifs. from math import* def u(n): u = 1.0 v = 1 if n > 1: for i in range(2,n+1): w = v v = u u = u+w return u print(u(10)/u(9)) print(u(22)/u(21)) print(u(100)/u(99)) print((1+sqrt(5))/2) On peut alors conjecturer que $\displaystyle{\lim_{n\rightarrow+\infty}\dfrac{u_{n+1}}{u_n}} = \varphi$.

Pour déterminer l'expression de $u_n$ en fonction de $n$, nous alors avoir besoin d'utiliser la formule : $\varphi^3=\varphi^2+\varphi$, qui provient directement de $\varphi^2=\varphi+1$.

Mais on peut la montrer avec de laborieux calculs comme ci-dessous, en cherchant à obtenir :

$\left(\dfrac{1+\sqrt{5}}{2}\right)^3$ $=$ $\left(\dfrac{1+\sqrt{5}}{2}\right)^2+\dfrac{1+\sqrt{5}}{2}$.

On utilise alors : $(a+b)^3$ $=$ $a^3+3a^2b+3ab^2+b^3$.

On a d'une part :
$\left(\dfrac{1+\sqrt{5}}{2}\right)^3$ $=$ $\dfrac{\left( 1+\sqrt{5} \right)^3}{8}$
$=$ $\dfrac{1}{8}\left( 1^3+3\times1^2\times\sqrt{5}+3\times1\times\sqrt{5}^2+\sqrt{5}^3 \right)$
$=$ $\dfrac{1}{8}\left( 1+3\sqrt{5}+15+5\sqrt{5} \right)$
$=$ $\dfrac{1}{8}\left( 16+8\sqrt{5} \right)$
$=$ $2+\sqrt{5}$.
D'autre part :
$\left(\dfrac{1+\sqrt{5}}{2}\right)^2+\dfrac{1+\sqrt{5}}{2}$ $=$ $\dfrac{1}{4}\left( 1+2\sqrt{5}+\sqrt{5}^2 \right)+\dfrac{1}{2}\left( 1+\sqrt{5} \right)$
$=$ $\dfrac{1}{4}\left( 6+2\sqrt{5}\right)+\dfrac{1}{2}\left( 1+\sqrt{5} \right)$
$=$ $\dfrac{1}{2}\left( 3+\sqrt{5}\right)+\dfrac{1}{2}\left( 1+\sqrt{5} \right)$
$=$ $\dfrac{1}{2}\left( 3+\sqrt{5}+ 1+\sqrt{5} \right)$
$=$ $\dfrac{1}{2}\left( 4+2\sqrt{5}\right)$
$=$ $2+\sqrt{5}$.
Ainsi, on a bien :

$\left(\dfrac{1+\sqrt{5}}{2}\right)^3$ $=$ $\left(\dfrac{1+\sqrt{5}}{2}\right)^2+\dfrac{1+\sqrt{5}}{2}$.

On démontrerait de même que :

$\left(\dfrac{1-\sqrt{5}}{2}\right)^3$ $=$ $\left(\dfrac{1-\sqrt{5}}{2}\right)^2+\dfrac{1-\sqrt{5}}{2}$.

On va alors pouvoir montrer par récurrence que :

pour tout entier $n\geq1$, $\:u_n=\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+1} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+1} \right)$.

Initialisation
Pour $n=0$, on sait que $u_0=1$.

Or,
$\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{0+1} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{0+1} \right)$ $=$ $\dfrac{1}{\sqrt{5}} \left( \dfrac{1+\sqrt{5}}{2} - \dfrac{1-\sqrt{5}}{2} \right)$
$=$ $\dfrac{1}{\sqrt{5}} \left( \dfrac{1+\sqrt{5}-1+\sqrt{5}}{2} \right)$
$=$ $\dfrac{1}{\sqrt{5}} \times \dfrac{2\sqrt{5}}{2} $
$=$ $1$.
L'égalité est donc vraie pour $n=0$.

Hérédité
On suppose que pour un certain entier $n$ :

$u_n=\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+1} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+1} \right)$,

et

$u_{n+1}=\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+2} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+2} \right)$.

On cherche alors à montrer que :

$u_{n+2}=\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+3} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+3} \right)$.

On sait que :
$u_{n+2}$ $=$ $u_{n+1}+u_{n}$
$=$ $\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+2} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+2} \right)+\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+1} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+1} \right)$
$=$ $\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+2} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+2} + \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+1} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+1} \right)$
$=$ $\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n}\left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{2}+ \dfrac{1+\sqrt{5}}{2} \right) - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n}\left( \left( \dfrac{1-\sqrt{5}}{2} \right)^{2}+ \dfrac{1-\sqrt{5}}{2} \right) \right) $
$=$ $\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n}\times \left( \dfrac{1+\sqrt{5}}{2} \right)^{3} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n}\times \left(\dfrac{1-\sqrt{5}}{2} \right)^{3} \right) $ D'après la question précédente
$=$ $\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+3} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+3} \right) $


Conclusion
D'après le principe de récurrence, pour tout $n\geq1$,

$u_n=\dfrac{1}{\sqrt{5}} \left( \left( \dfrac{1+\sqrt{5}}{2} \right)^{n+1} - \left( \dfrac{1-\sqrt{5}}{2} \right)^{n+1} \right)$.


Nous allons maintenant pouvoir étudier la limite de $w_n=\dfrac{u_{n+1}}{u_n}$.
On note $\psi = \dfrac{1-\sqrt{5}}{2}$ et on obtient alors :
$w_n$ $=$ $\dfrac{u_{n+1}}{u_n}$
$=$ $\dfrac{\dfrac{1}{\sqrt{5}} \left( \varphi^{n+2} - \psi^{n+2} \right)}{\dfrac{1}{\sqrt{5}} \left( \varphi^{n+1} - \psi^{n+1} \right)}$
$=$ $\dfrac{ \varphi^{n+2} - \psi^{n+2} }{ \varphi^{n+1} - \psi^{n+1}}$
$=$ $\dfrac{ \varphi^{n+2}\left(1 - \dfrac{\psi^{n+2}}{\varphi^{n+2}}\right) }{\varphi^{n+1}\left(1 - \dfrac{\psi^{n+1}}{\varphi^{n+1}}\right)}$
$=$ $\dfrac{ \varphi\left(1 - \left(\dfrac{\psi}{\varphi}\right)^{n+2}\right) }{1 - \left(\dfrac{\psi}{\varphi}\right)^{n+1}}$
$=$ $\dfrac{ \varphi\left(1 - \left(\dfrac{1-\sqrt{5}}{1+\sqrt{5}}\right)^{n+2} \right) }{1 - \left(\dfrac{1-\sqrt{5}}{1+\sqrt{5}}\right)^{n+1}}$.
Or, $\dfrac{1-\sqrt{5}}{1+\sqrt{5}}\approx-0,38\in]-1\,;1[$ et donc $\displaystyle{\lim_{n\rightarrow+\infty}\left(\dfrac{1-\sqrt{5}}{1+\sqrt{5}}\right)^{n+2}=0}$ et $\displaystyle{\lim_{n\rightarrow+\infty}\left(\dfrac{1-\sqrt{5}}{1+\sqrt{5}}\right)^{n+1}=0}$.

Ainsi, on peut conclure que $\displaystyle{\lim_{n\rightarrow+\infty}\dfrac{u_{n+1}}{u_n}}$ $=$ $\dfrac{\varphi(1-0)}{1-0}$ $=$ $\varphi$.

La suite de Fibonacci converge bien vers le nombre d'or. Les ratios de Fibonacci Les rapports entre deux termes consécutifs de la suite de Fibonacci étudiée précédemment s'appellent les ratios de Fibonacci. Les ratios entre un terme de la suite et le suivant converge vers l'inverse du nombre d'or (cf paragraphe précédent).
On définit les ratios de retracement à partir des puissance négatives du nombre d'or limite donc de la suite de Fibonacci.

Par exemple :
$\varphi^0=1$,
$\varphi^{-1/2}\approx 0,786$,
$\varphi^{-1}\approx 0,618$,
$\varphi^{-2}\approx 0,382$,
$\varphi^{-3}\approx 0,236$,
et $\displaystyle{\lim_{n\rightarrow+\infty}\varphi^{-n}=0}$.

On définit à partir de ces valeurs les ratios de retracement : $0$ - $0,236$ - $0,382$ - $0,50$ - $0,618$ - $0,786$ - $1$.

Ralph Nelson Elliott (1871 - 1948) comptable et spécialiste des marchés financiers a élaboré la célébre théorie des vagues d'Elliot basée sur les ratios de Fibonacci.
Dans sa théorie, Ralph Nelson Elliott fait référence à trois phénomènes importants qui caractérisent les mouvements des marchés financiers : la forme qu'ils décrivent, leur amplitude et leur durée. La forme est analogue à une progression par vagues successives tandis que l'amplitude (qui sépare les points d'amorce et de terminaison des vagues) est prédictible notamment avec les ratios de retracement de Fibonacci décrits ci-dessus.
L'objectif est de prévoir l'évolution d'un titre ou d'un indice boursier, et d'analyser au sein d'une tendance principale des phases opposées. La méthode utilisée, et qui découle de la théorie des vagues d'Elliot, s'appelle méthode de retracements de Fibonnaci. Elle permet de déterminer des objectifs de cours au sein de phases de consolidation et de prévoir l’amplitude des corrections et des rebonds afin de se positionner au mieux au sein d’une tendance.
Il est à noter que tous les analystes et les traders de la planète regardent les ratios de Fibonacci, ils ont donc de fait un caractère auto-réalisateur.