La tige métalique plantée au centre du cadran s'appelle un
À savoir également qu'un cadran solaire indique l'heure solaire et non pas l'heure de nos montres (c'est-à-dire l'heure moyenne).
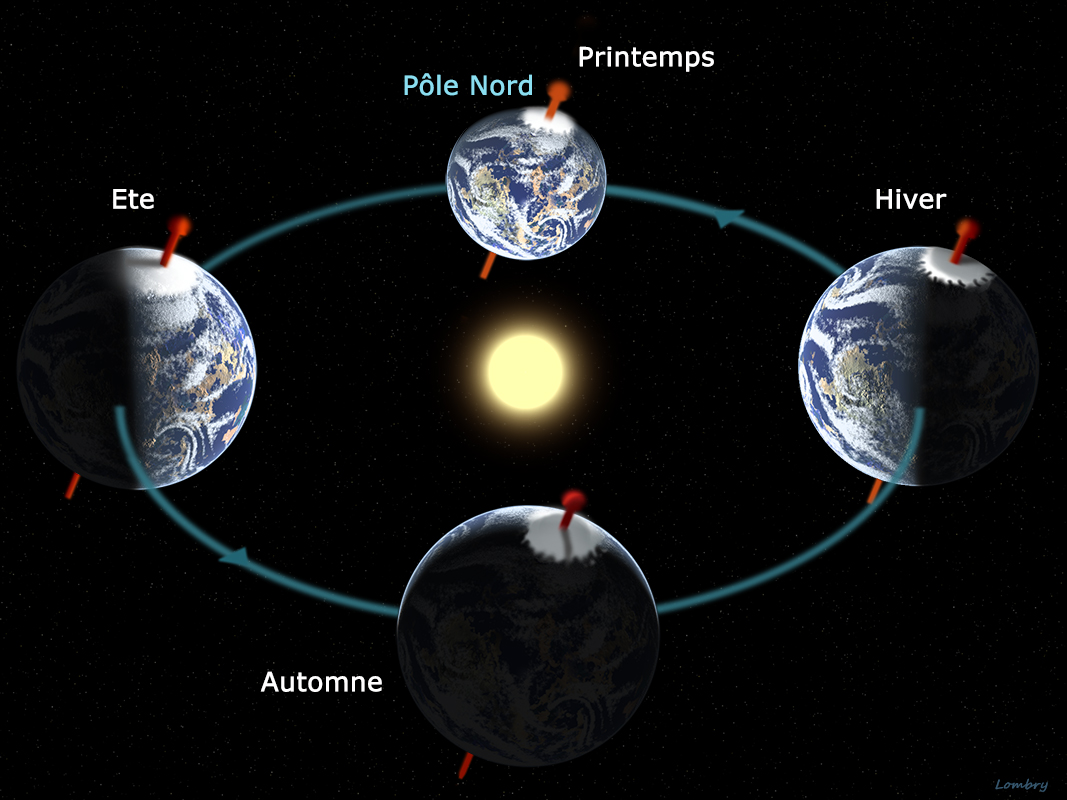
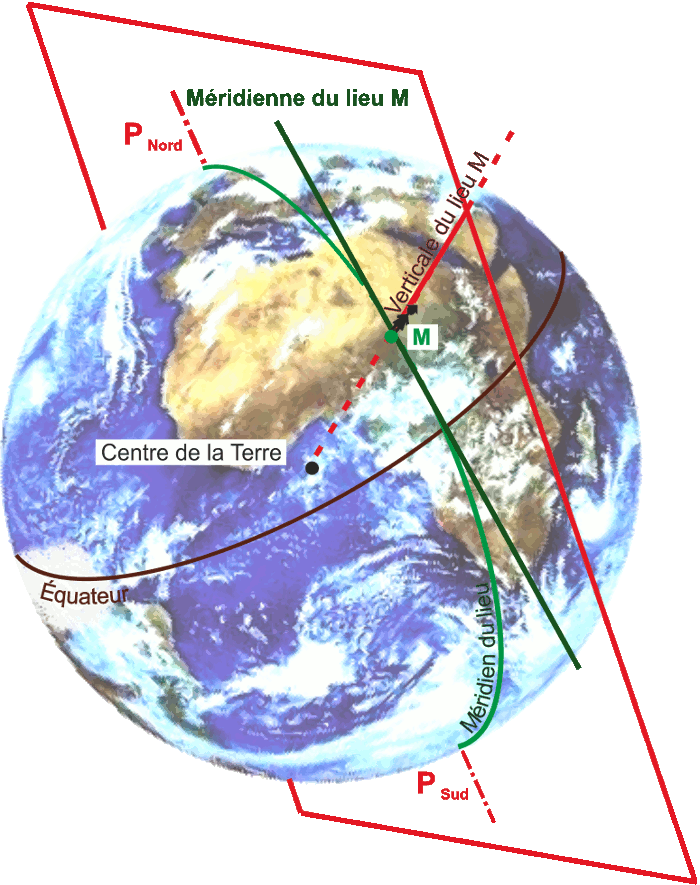
Par exemple, le midi solaire, en un lieu donné sur Terre, est le moment de la journée où le soleil est au plus haut dans le ciel. En terme géométrique, cela correspond au moment où le soleil passe dans le plan méridien du lieu.

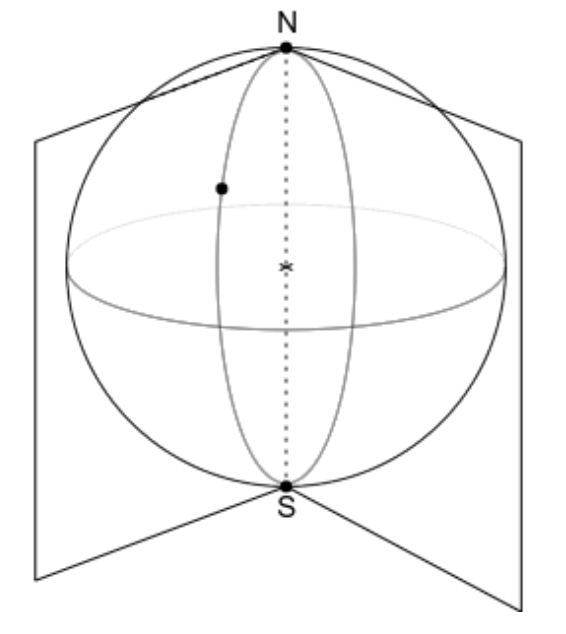
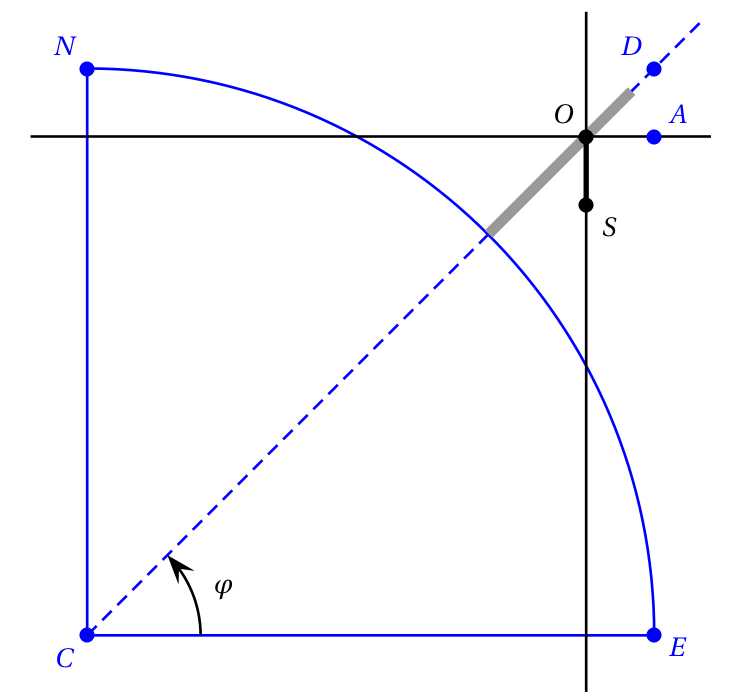
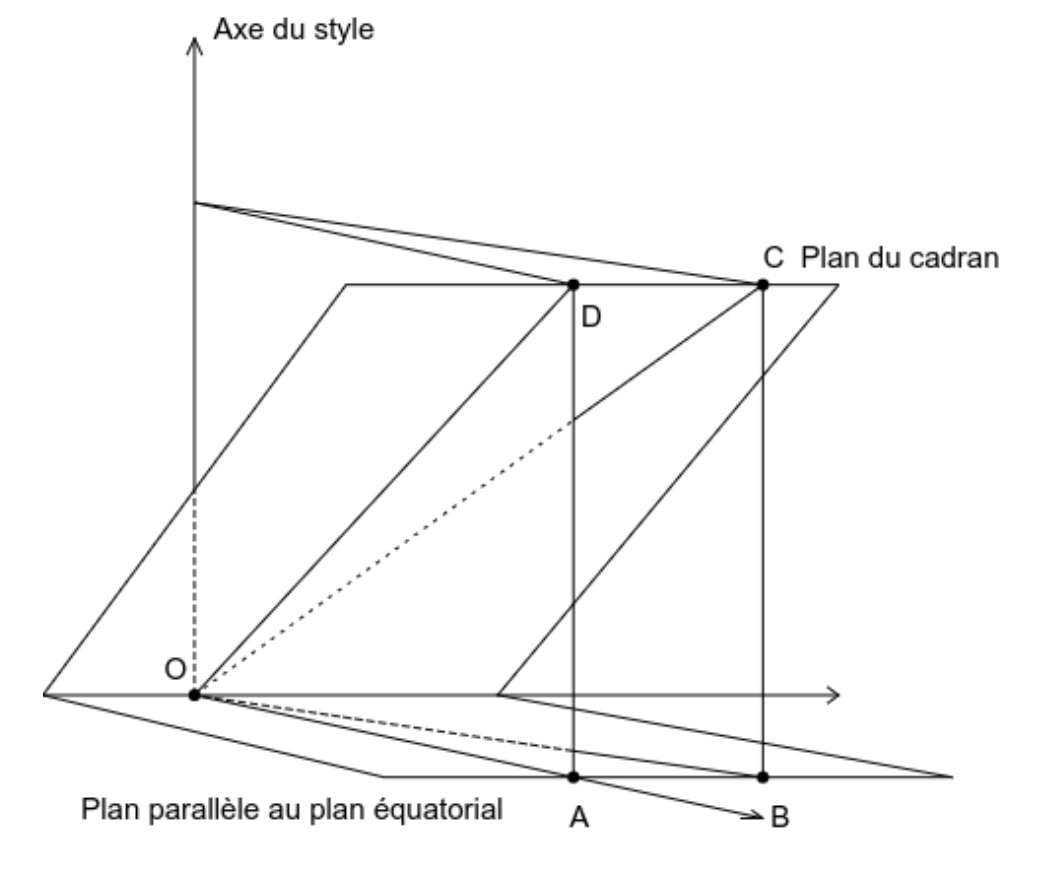 On reprend les notations de la figure précédente. Le plan $OAD$ est le plan méridien de midi et le plan $OBC$ est un autre plan méridien. Les droites $(AD)$ et $(BC)$ sont parallèles à l'axe du style et les droites $(AB)$ et $(DC)$ sont parallèles.
On reprend les notations de la figure précédente. Le plan $OAD$ est le plan méridien de midi et le plan $OBC$ est un autre plan méridien. Les droites $(AD)$ et $(BC)$ sont parallèles à l'axe du style et les droites $(AB)$ et $(DC)$ sont parallèles.
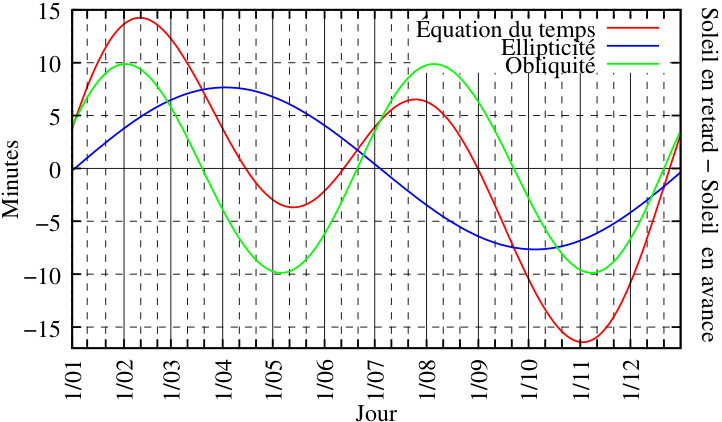 Il existe un enchaînement de formules « simplifiées » pour déterminer les valeurs de l'équation du temps :
Il existe un enchaînement de formules « simplifiées » pour déterminer les valeurs de l'équation du temps :