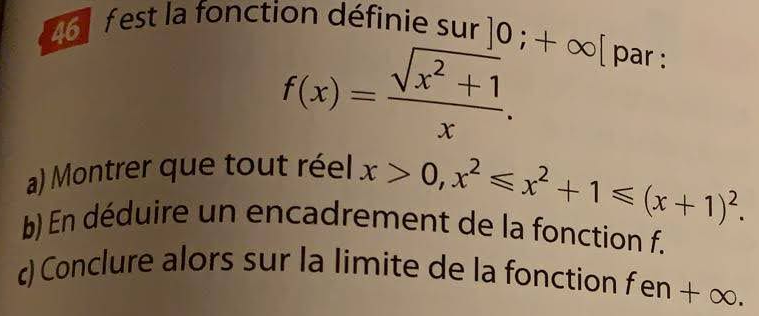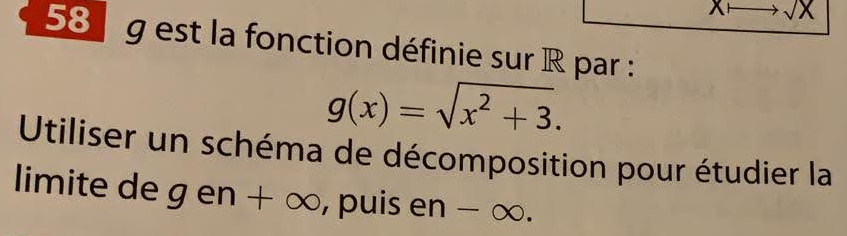Limites de fonctions ∼ Exercices
Exercice 26
 x→−∞limf(x) = −∞.
x→−∞limf(x) = −∞.
x→+∞limf(x) = +∞.
Exercice 27
 x→−∞limf(x) = −1.
x→−∞limf(x) = −1.
x→+∞limf(x) = 3.
Exercice 32
 On étudie les limites aux bornes de l'ensemble de définition : ]−∞;−1[∪]−1;1[∪]1;+∞[.
On étudie les limites aux bornes de l'ensemble de définition : ]−∞;−1[∪]−1;1[∪]1;+∞[.
Exercice 33
 x→1−limf(x) = −∞
x→1−limf(x) = −∞
x→1+limf(x) = +∞
Exercice 38

Exercice 39

Exercice 40

Exercice 48
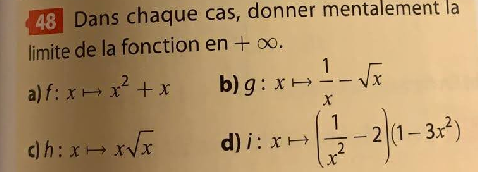
Exercice 49
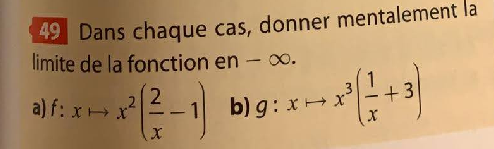
Exercice 64
 x→+∞lim7−ex = −∞.
x→+∞lim7−ex = −∞.
x→−∞limf(x) = 7
Exercice 65
 x→+∞limf(x) = x→+∞lim31×xex = +∞, par croissances comparées.
x→+∞limf(x) = x→+∞lim31×xex = +∞, par croissances comparées.
x→+∞limexx = 0.
Exercice 30

Exercice 36

Exercice 37

Exercice 41

Exercice 42

Exercice 44

Exercice 46
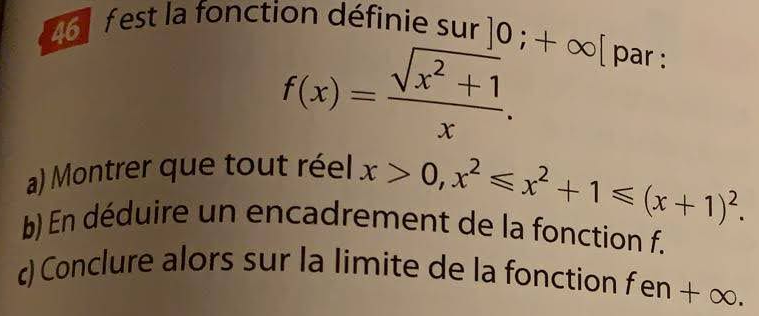
Exercice 47

Exercice 58
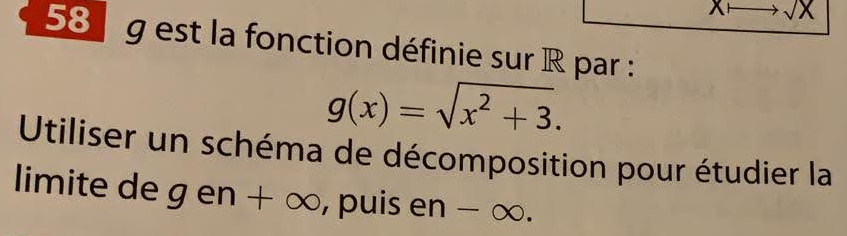
Exercice 59

Exercice 60

Exercice 61

Exercice 62

Exercice 63

Exercice 68

Exercice 72

Exercice 74 à 77

Exercice 90

Exercice 95

Exercice 104

 .
.
 .
.
 On étudie les limites aux bornes de l'ensemble de définition : .
On étudie les limites aux bornes de l'ensemble de définition : .




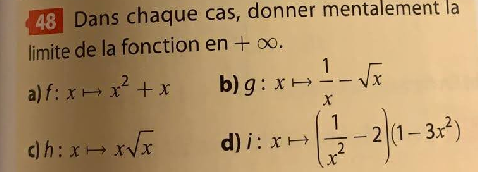
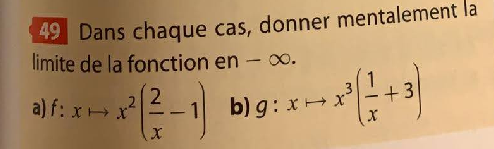
 .
.
 , par croissances comparées.
, par croissances comparées.